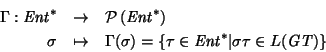.
Las operaciones matriciales son congruentes con ``particiones por bloques'', es decir, si se parte a dos matrices
.
Las operaciones matriciales son congruentes con ``particiones por bloques'', es decir, si se parte a dos matrices
 como
como
 ,
diremos que
,
diremos que
 ,
siempre que
,
siempre que
 y una partición de ella por bloques
y una partición de ella por bloques
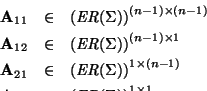
 y
y
 .
Por tanto,
.
Por tanto,
 .
Por tanto,
.
Por tanto,
 y
y
 .
Más aún, si
.
Más aún, si
 ,
,
 ,
,
![\begin{displaymath}\mbox{\bf A}_4=\left[\begin{array}{cccc}
a_{11} & a_{12} & ...
...34} \\
a_{41} & a_{42} & a_{43} & a_{44}
\end{array}\right]\end{displaymath}](img1384.gif)