


Siguiente: Programas
Un nivel arriba: Series de potencias e
Anterior: Series sobre los racionales
Para una gramática libre de contexto
G=(V,T,P,s0), su serie generativa puede hacérse corresponder con una serie en
![$I\!\!\!\!Q[[V\cup T]]$](img2068.gif) de manera que las ecuaciones impuestas por las producciones en P se satisfagan también en
de manera que las ecuaciones impuestas por las producciones en P se satisfagan también en
![$I\!\!\!\!Q[[V\cup T]]$](img2068.gif) .
En efecto, a cada símbolo s en
.
En efecto, a cada símbolo s en 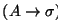 asociémosle una incógnita Xs. Sea
asociémosle una incógnita Xs. Sea
![$\mbox{\bf X}=[X_s\vert s\in V\cup T]$](img2069.gif) .
Tratemos ahora el producto de incógnitas como si fuera conmutativo, pues de hecho lo es en
.
Tratemos ahora el producto de incógnitas como si fuera conmutativo, pues de hecho lo es en
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) .
Con esto, la serie generativa pL de L(G) corresponde con una serie
.
Con esto, la serie generativa pL de L(G) corresponde con una serie 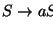 en
en
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) .
Observamos dos características:
.
Observamos dos características:
- la serie generativa no involucra a los símbolos de V, pues esta serie se expande hasta la supresión de los símbolos variables, y
- todas las palabras que son permutaciones de un mismo ``multiconjunto'' se símbolos corresponden a un mismo monomio en
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) :
:
Consecuentemente, el coeficiente de un monomio en la serie 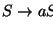 es el número de posibles árboles de derivación derivables en G correspondientes a una palabra sobre el multiconjunto correspondiente al monomio.
Esta transformación da así un método para contar derivaciones. Si la gramática no es ambigua, entonces cada palabra del lenguaje corresponde a un único árbol y, consecuentemente, éste procedimiento cuenta palabras generadas.
Ejemplos.
1. Para la gramática que genera palíndromas pares (
es el número de posibles árboles de derivación derivables en G correspondientes a una palabra sobre el multiconjunto correspondiente al monomio.
Esta transformación da así un método para contar derivaciones. Si la gramática no es ambigua, entonces cada palabra del lenguaje corresponde a un único árbol y, consecuentemente, éste procedimiento cuenta palabras generadas.
Ejemplos.
1. Para la gramática que genera palíndromas pares (
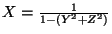 )
o sea
S=aSa+bSb+1 consideremos la correspondencia inducida por
)
o sea
S=aSa+bSb+1 consideremos la correspondencia inducida por
La producción da la ecuación
X=YXY+ZYZ+1=X(Y2+Z2)+1
y por tanto
 .
La serie
.
La serie 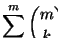 correspondiente a la serie generativa ha de ser solución de esta última ecuación. Por tanto, según se vió en la proposición 6.5.2 de la anterior sección,
correspondiente a la serie generativa ha de ser solución de esta última ecuación. Por tanto, según se vió en la proposición 6.5.2 de la anterior sección,
Así pues para cada 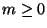 hay
hay
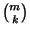 posibles árboles para palabras de longitud 2m, y para cada
posibles árboles para palabras de longitud 2m, y para cada 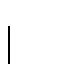 hay
hay
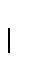 árboles para palabras de longitud 2m con 2k apariciones del símbolo b.
Como la gramática no es ambigua, la cuenta de árboles correponde a la cuenta de palabras.
árboles para palabras de longitud 2m con 2k apariciones del símbolo b.
Como la gramática no es ambigua, la cuenta de árboles correponde a la cuenta de palabras.
2. Para la gramática de cadenas equilibradas de paréntesis [
 ]
o sea
S=()+(S)+SS consideremos la correspondencia inducida por
]
o sea
S=()+(S)+SS consideremos la correspondencia inducida por
La producción da la ecuación
y por tanto
 .
Consideremos por un momento Z=1. Entonces tenemos la ecuación 6.2 de la sección anterior. Consecuentemente, X tiene dos soluciones de la forma
.
Consideremos por un momento Z=1. Entonces tenemos la ecuación 6.2 de la sección anterior. Consecuentemente, X tiene dos soluciones de la forma
 donde b0=0,1 y
donde b0=0,1 y
En nuestro caso no hay ninguna paabra equilibrada con 0 paréntesis derechos. Así pues, el término independiente de la serie generativa debe ser b0=0. Con esta elección de b0 se tiene determinados a los demás coeficientes bm. Cada uno de ellos da el número de árboles de derivación de cadenas equilibradas de paréntesis para formar cadenas equilibradas con m paréntesis derechos.
Como la gramática es ambigua el número de árboles excede el de cadenas equilibradas.
3. Consideremos la gramática con producciones
El lenguaje generado por la gramática es
La gramática se expresa por la ecuación S=SbS+a y mediante la correspondencia
se tiene la ecuación X=YX2+1.
Al resolverla con la fórmula de Lagrange 6.3 se tiene
Para cada 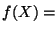 se tiene
se tiene
Al evaluar en el punto x=1 obtenemos
lo cual significa que para cada m hay
derivaciones de la única palabra (ab)ma generable en la gramática que contiene exactamente m b's.



Siguiente: Programas
Un nivel arriba: Series de potencias e
Anterior: Series sobre los racionales
Guillermo Morales-Luna
2000-06-27
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) :
:
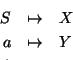
![$\mbox{\bf X}=[X_s\vert s\in V\cup T]$](img2069.gif) .
Tratemos ahora el producto de incógnitas como si fuera conmutativo, pues de hecho lo es en
.
Tratemos ahora el producto de incógnitas como si fuera conmutativo, pues de hecho lo es en
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) .
Con esto, la serie generativa pL de L(G) corresponde con una serie
.
Con esto, la serie generativa pL de L(G) corresponde con una serie ![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) .
Observamos dos características:
.
Observamos dos características:
![$I\!\!\!\!Q[[\mbox{\bf X}]]$](img2010.gif) :
:
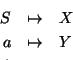
 .
La serie
.
La serie  hay
hay
 árboles para palabras de longitud 2m con 2k apariciones del símbolo b.
Como la gramática no es ambigua, la cuenta de árboles correponde a la cuenta de palabras.
árboles para palabras de longitud 2m con 2k apariciones del símbolo b.
Como la gramática no es ambigua, la cuenta de árboles correponde a la cuenta de palabras.
 ]
o sea
S=()+(S)+SS consideremos la correspondencia inducida por
]
o sea
S=()+(S)+SS consideremos la correspondencia inducida por
 donde b0=0,1 y
donde b0=0,1 y
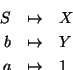
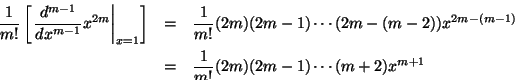
![\begin{displaymath}X=1+\sum_{m\geq 1} \frac{1}{m!}\left[\left.\frac{\textstyle d^{m-1}}{\textstyle dx^{m-1}}x^{2m}\right\vert _{x=1}\right] Y^m.\end{displaymath}](img2087.gif)