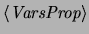Posterior: Deducción natural Arriba: Cálculo proposicional booleano Anterior: Cálculo proposicional booleano

Reglas convencionales de buena formación

Como es convencional, los conectivos tienen asociada una prioridad:

$$\begin{array}{\vert\vert c\vert l\vert\vert}\hline \hline \m... ...3 & \rightarrow,\leftrightarrow \\ \hline \hline \end{array}$$

donde un valor menor de Prior significa que el correspondiente conectivo se aplica más rápido, y, en igualdad de prioridades, el orden de izquierda a derecha determina el de aplicación de los conectivos. Así,

$$\neg x_a\lor x_2\land x_3\lor x_5\rightarrow x_6\leftrightarrow x_7$$

se ha de interpretar como

$$\left[\left(\left(\neg x_a\lor x_2\right)\land x_3\right)\lor x_5\rightarrow x_6\right]\leftrightarrow x_7.$$

Introduzcamos entonces los siguientes símbolos variables para la gramática formal:

$\langle\mbox{\it VarsProp}\rangle$	: variables proposicionales,
$\langle\mbox{\it Prop}\rangle$	: proposiciones bien formadas,
$\langle\mbox{\it PropNeg}\rangle$	: proposiciones cuyo conectivo principal es la negación,
$\langle\mbox{\it PropCon}\rangle$	: proposiciones cuyo conectivo principal es la conjunción,
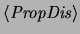$\langle\mbox{\it PropDis}\rangle$	: proposiciones cuyo conectivo principal es la disyunción,
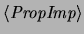$\langle\mbox{\it PropImp}\rangle$	: proposiciones cuyo conectivo principal es la implicación,
$\langle\mbox{\it PropEqu}\rangle$	: proposiciones cuyo conectivo principal es la equivalencia.
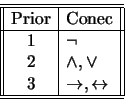
$\langle\mbox{\it Prop1}\rangle$	: proposiciones cuyo conectivo principal tiene prioridad 1,
$\langle\mbox{\it Prop2}\rangle$	: proposiciones cuyo conectivo principal tiene prioridad 2,
$\langle\mbox{\it Prop3}\rangle$	: proposiciones cuyo conectivo principal tiene prioridad 3,

En la tabla 2.10 presentamos las producciones de la gramática $\mbox{\rm Pbf}_B(X)$ (de Proposiciones Bien Formadas).

Table 2.10: Gramática de proposiciones bien formadas.

El lenguaje generado por $\mbox{\rm Pbf}_B(X)$ consta de todas las proposiciones bien formadas a partir de las variables proposicionales $x_1,\ldots, x_n$.


Ejemplo. La cadena de caracteres

$$\phi:= (\neg x_1 \rightarrow x_2\lor \neg x_3 \land x_4) \leftrightarrow x_5$$

sobre el alfabeto del Cálculo Proposicional, es una proposición. En efecto, se tiene $\phi:= \phi_1\leftrightarrow \phi_2$ donde las dos proposiciones componentes quedan vistas como tales en la tabla 2.11.

Table 2.11: Ejemplos de proposiciones bien formadas.

$\quad\Box$ Así nos adaptaremos a nuestras propias convenciones en la lectura de proposiciones y fórmulas lógicas. Sin embargo esta decisión es irrelevante desde el punto de vista de la lógica y pudimos haber adoptado la notación polaca inversa, pues ambas notaciones son completamente equivalentes. Insistimos, los tres sistemas de representación de proposiciones $\mbox{\rm Pbf}_B(X)$, $\mbox{\rm Pbf}(X)$ y $\mbox{\rm Pbf}_H(X)$ son equivalentes y reductibles cada uno a cualquier otro. Desde el punto de vista lógico es preferible $\mbox{\rm Pbf}_H(X)$ por su sencillez; por comodidad en la lectura de proposiciones, en lo que queda de esta sección utilizaremos $\mbox{\rm Pbf}(X)$. Sin embargo el más utilizado en la práctica, y por nosotros en la mayor parte del presente texto, es $\mbox{\rm Pbf}_B(X)$.
Posterior: Deducción natural Arriba: Cálculo proposicional booleano Anterior: Cálculo proposicional booleano