Si
![]() son sendos
son sendos ![]() -uplos de vectores de
-uplos de vectores de ![]() , vale para dichas estructuras:
, vale para dichas estructuras:
Demostración
Siendo ![]() un isomorfismo lineal de
un isomorfismo lineal de ![]() sobre
sobre ![]() , por el corolario del teorema 1.4.7
, por el corolario del teorema 1.4.7
![]() es un isomorfismo
del espacio vectorial
es un isomorfismo
del espacio vectorial
![]() sobre su dual
sobre su dual
![]() .
También por el teorema 2.3.3:
.
También por el teorema 2.3.3:
En virtud del teorema 3.1.4, induce sobre el espacio vectorial
![]() una estructura de espacio de producto escalar, siendo:
una estructura de espacio de producto escalar, siendo:
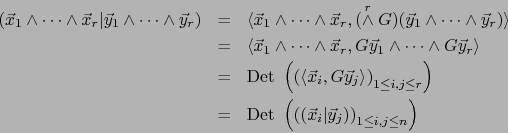
Observación 1.
Puesto que
![]() es la identidad sobre
es la identidad sobre
![]() , el producto escalar de dos elementos
, el producto escalar de dos elementos
![]() es
es ![]() , el producto usual en
, el producto usual en ![]() .
.
Observación 2.
Sean
![]() y
y
![]() una base de
una base de ![]() y la base de
y la base de ![]() dual de ésta. Sean
dual de ésta. Sean
![]() y
y
![]() las bases de sendos espacios
las bases de sendos espacios
![]() asociadas a las anteriores.
Por el teorema 1.4.19 tenemos:
asociadas a las anteriores.
Por el teorema 1.4.19 tenemos:
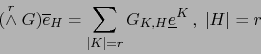
Demostración
En virtud del teorema 3.1.13 basta probar la primera afirmación. Sea
![]() una base O.N. de
una base O.N. de ![]() . Sean
. Sean ![]() partes de
partes de
![]() de cardinalidad
de cardinalidad ![]() :
:
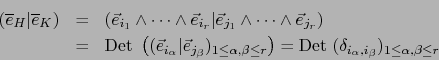
Otra demostración.
Usamos la condición 2 después de las definiciones 3.1.7. Por ella vale:
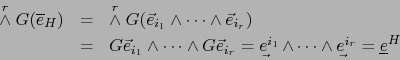
La aplicación
![]() (la notaremos simplemente
(la notaremos simplemente
![]() ) es un isomorfismo simétrico del espacio vectorial
) es un isomorfismo simétrico del espacio vectorial
![]() sobre su dual
sobre su dual
![]() . Define sobre
. Define sobre
![]() una estructura de espacio de producto escalar dicha ESTRUCTURA DE ESPACIO DE PRODUCTO ESCALAR INDUCIDA por la de
una estructura de espacio de producto escalar dicha ESTRUCTURA DE ESPACIO DE PRODUCTO ESCALAR INDUCIDA por la de ![]() .
.
![]() es una isometría de
es una isometría de
![]() sobre
sobre
![]() y
y
![]() es la
isometría inversa de
es la
isometría inversa de
![]() sobre
sobre
![]() .
.
Si
![]() son dos
son dos ![]() -uplos de covectores, elementos de
-uplos de covectores, elementos de ![]() vale:
vale:
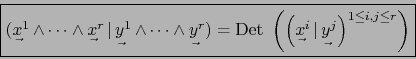
Demostración
Por el teorema 3.2.1 la aplicación
![]() es un isomorfismo simétrico del espacio vectorial
es un isomorfismo simétrico del espacio vectorial
![]() sobre su dual. Por el corolario del teorema 1.4.7 la aplicación inversa de ésta es
sobre su dual. Por el corolario del teorema 1.4.7 la aplicación inversa de ésta es
![]() . Como hemos dicho, la notaremos simplemente
. Como hemos dicho, la notaremos simplemente
![]() .
.
Por el teorema 3.1.5, dicha inversa
![]() es un isomorfismo simétrico del espacio vectorial
es un isomorfismo simétrico del espacio vectorial
![]() sobre su dual
sobre su dual
![]() . Define sobre
. Define sobre
![]() una estructura de espacio de producto escalar.
una estructura de espacio de producto escalar.
Por la fórmula (2) en la demostración del teorema 3.1.5 vale:
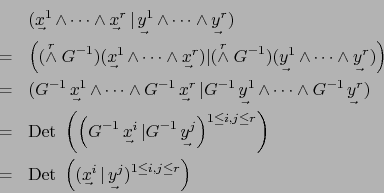
Observación
Sean
![]() una base de
una base de ![]() y
y
![]() las bases asociadas de sendos espacios vectoriales
las bases asociadas de sendos espacios vectoriales
![]() . Por el teorema 1.4.19 las relaciones:
. Por el teorema 1.4.19 las relaciones:
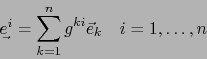
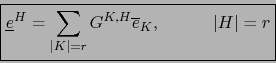
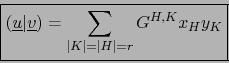
Demostración
En virtud del teorema 3.1.13, basta probar la primera afirmación.
Sea
![]() una base O.N. de
una base O.N. de ![]() . Por el teorema 3.2.2,
. Por el teorema 3.2.2,
![]() es una base O.N. de
es una base O.N. de
![]() . Pero por el teorema 2.3.1 la base
. Pero por el teorema 2.3.1 la base
![]() de
de
![]() es la base dual de la base
es la base dual de la base
![]() de
de
![]() . Luego por el teorema 3.1.16, la base
. Luego por el teorema 3.1.16, la base
![]() es una base O.N. de
es una base O.N. de
![]() .
.
![]()
Demostración
Por la observación después de la definición 3.1.4 y el teorema 2.3.2 tenemos:
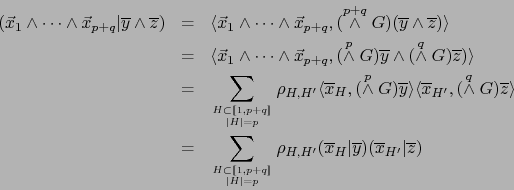
Demostración
Puesto que
![]() es una isometría de
es una isometría de
![]() sobre
sobre
![]() tenemos:
tenemos:
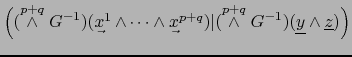 |
|||
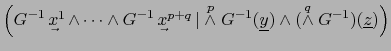 |
(4) | ||