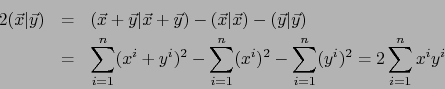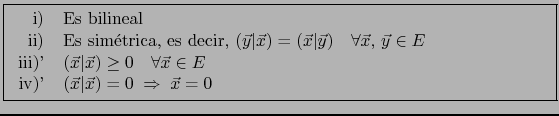
El espacio vectorial real ![]() junto con tal aplicación se llama ESPACIO VECTORIAL EUCLIDIANO.
Por abuso de lenguaje se habla del ``espacio vectorial euclidiano
junto con tal aplicación se llama ESPACIO VECTORIAL EUCLIDIANO.
Por abuso de lenguaje se habla del ``espacio vectorial euclidiano ![]() ''.
''.
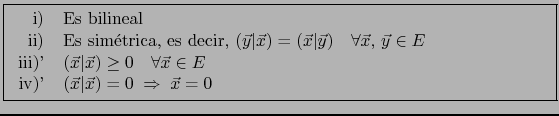
El espacio vectorial real ![]() junto con tal aplicación se llama ESPACIO VECTORIAL EUCLIDIANO.
Por abuso de lenguaje se habla del ``espacio vectorial euclidiano
junto con tal aplicación se llama ESPACIO VECTORIAL EUCLIDIANO.
Por abuso de lenguaje se habla del ``espacio vectorial euclidiano ![]() ''.
''.
Notamos que la aplicación
![]() que satisface i), ii), iii)', iv)' es un producto escalar sobre
que satisface i), ii), iii)', iv)' es un producto escalar sobre ![]() .
.
En efecto, sea ![]() tal que:
tal que:
![]() . En particular vale
. En particular vale
![]() de donde, por el axioma iv)'
de donde, por el axioma iv)' ![]() . Se cumple pues el axioma iii) de producto escalar (o sea nuestro producto es no degenerado).
. Se cumple pues el axioma iii) de producto escalar (o sea nuestro producto es no degenerado).
Así pues, un espacio vectorial euclidiano es un caso particular de un espacio de producto escalar.
El axioma iv)' dice que un espacio vectorial euclidiano no posee ningún vector isótropo.
Observación
Sean ![]() un espacio vectorial euclidiano y
un espacio vectorial euclidiano y ![]() un subespacio arbitrario de
un subespacio arbitrario de ![]() . La restricción del producto escalar
. La restricción del producto escalar
![]() a
a ![]() satisface los axiomas i), ii), iii)', iv)' luego hace de
satisface los axiomas i), ii), iii)', iv)' luego hace de ![]() un espacio vectorial euclidiano.
un espacio vectorial euclidiano.
Es la única estructura de espacio vectorial euclidiano sobre ![]() que consideraremos. Diremos simplemente que un subespacio
que consideraremos. Diremos simplemente que un subespacio ![]() de un espacio vectorial euclidiano
de un espacio vectorial euclidiano ![]() es también un espacio vectorial euclidiano.
es también un espacio vectorial euclidiano.
Advertencia
Una propiedad análoga a la precedente no rige en espacios de producto escalar generales. Si ![]() es un espacio de un espacio
es un espacio de un espacio ![]() de producto escalar, la restricción del producto escalar a
de producto escalar, la restricción del producto escalar a ![]() no satisface en general el axioma iii) de producto escalar. He aquí un contraejemplo:
no satisface en general el axioma iii) de producto escalar. He aquí un contraejemplo:
Sea ![]() un espacio vectorial de dimensión 2 sobre un cuerpo
un espacio vectorial de dimensión 2 sobre un cuerpo ![]() , provisto de una base
, provisto de una base
![]() . Si
. Si
![]() e
e
![]() definimos:
definimos:
Demostración
Por el teorema 3.1.9 se verifica:
He aquí tres condiciones equivalentes a ésta:
Condición 1.
En presencia de la base
![]() :
:
Condición 2.
Condición 3.
![]() (resp.
(resp.
![]() ) las componentes covariantes de
) las componentes covariantes de ![]() (resp. de
(resp. de
![]() ) coinciden con las componentes contravariantes de
) coinciden con las componentes contravariantes de ![]() (resp. de
(resp. de
![]() ).
En otras palabras:
).
En otras palabras:
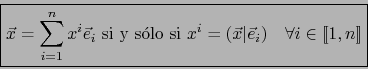
Advertencia
No todo espacio de producto escalar posee una base O.N. Esto será, por ejemplo, una consecuencia del teorema a continuación.
Demostración
A) Supongamos que ![]() posee una base O.N.
posee una base O.N.
![]() . Vale, pues:
. Vale, pues:
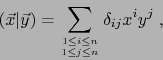
B) Recíprocamente, sea ![]() un espacio vectorial euclidiano. Probaremos la existencia de una base O.N. en
un espacio vectorial euclidiano. Probaremos la existencia de una base O.N. en ![]() por inducción sobre la dimensión
por inducción sobre la dimensión ![]() de
de ![]() .
.
Sea ![]() un vector arbitrario no nulo de
un vector arbitrario no nulo de ![]() . Definamos:
. Definamos:
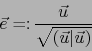
Sea ![]() un espacio vectorial euclidiano de dimensión
un espacio vectorial euclidiano de dimensión ![]() . Como en (i) determinamos un vector
. Como en (i) determinamos un vector
![]() tal que
tal que
![]() . Consideremos el subespacio
. Consideremos el subespacio
![]() de
de ![]() .
. ![]() es un espacio vectorial euclidiano de dimensión
es un espacio vectorial euclidiano de dimensión ![]() . Por hipótesis de inducción,
. Por hipótesis de inducción, ![]() posee una base O.N.
posee una base O.N.
![]() . Patentemente
. Patentemente
![]() es una base O.N. de
es una base O.N. de ![]() .
.
![]()
Generalicemos las definiciones 3.1.7.
Sea ![]() un espacio de producto escalar (sobre un cuerpo conmutativo arbitrario
un espacio de producto escalar (sobre un cuerpo conmutativo arbitrario ![]() ).
).
Demostración
Sean ![]() un espacio de producto escalar y
un espacio de producto escalar y
![]() una familia ortogonal de
una familia ortogonal de ![]() . Supongamos una relación lineal:
. Supongamos una relación lineal:
Demostración
Por el teorema 3.1.14 vale ![]() . Sea
. Sea ![]() el subespacio
el subespacio
![]() de
de ![]() .
. ![]() es un espacio vectorial euclidiano de dimensión
es un espacio vectorial euclidiano de dimensión ![]() . Por el teorema 3.1.12
. Por el teorema 3.1.12 ![]() posee una
base O.N.
posee una
base O.N.
![]() . Obviamente
. Obviamente
![]() es una
base O.N. de
es una
base O.N. de ![]() .
.
![]()
La parte a) de la demostración del teorema 3.1.13 invita a la siguiente:
Observación
Sea
![]() una base de un espacio de producto escalar E. Las afirmaciones siguientes
son equivalentes a pares:
una base de un espacio de producto escalar E. Las afirmaciones siguientes
son equivalentes a pares:

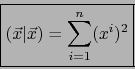
Demostración
Del cálculo en la parte a) de la demostración del teorema 3.1.13 (para el cual es inútil la
hipótesis
![]() ) se desprenden las implicaciones
) se desprenden las implicaciones
![]() y
y
![]() .
.
Implicación
![]() . Supongamos que
. Supongamos que
![]() implican
implican
![]() .
Al tomar
.
Al tomar
![]() o sea
o sea
![]() e
e
![]() o sea
o sea
![]() conseguimos:
conseguimos:
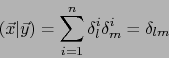
Implicación
![]() . Supongamos que
. Supongamos que
![]() vale:
vale: