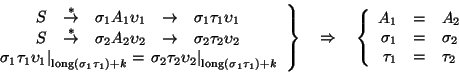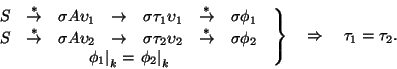Siguiente: Ejercicios Un nivel arriba: Gramáticas formales Anterior: Ejemplos

Tipos de gramáticas

En el estudio de las gramáticas formales y de sus correspondientes lenguajes aparecen varios problemas, entre los que se cuentan a los siguientes:

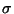
Problema 4.1 (de la Palabra)   Dada una gramática G y una palabra $\sigma$ sobre su alfabeto de símbolos terminales, decidir si acaso la palabra pertenece o no al lenguaje generado por G.

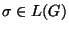
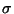
Problema 4.2 (de Derivación)   Dada una gramática G y una $\sigma\in L(G)$ encontrar una derivación en G de $\sigma$ a partir del símbolo inicial de G.

Problema 4.3 (Formalización de un lenguaje)   Dado un lenguaje L encontrar una gramática G tal que L(G)=L, es decir, tal que genere al lenguaje L.

Estos problemas pueden ser muy complejos, e irresolubles, en general, si consideramos como ``decidir'' el aplicar un procedimiento efectivo, en el sentido de Church, que en un número finito de transformaciones simbólicas nos dé una respuesta positiva o negativa al problema planteado. En toda clase de gramáticas es de suma importancia decidir la resolubilidad de los anteriores problemas y, en el caso de que sean resolubles, calcular la complejidad de los procedimientos para resolverlos. En la definición siguiente presentamos algunas clases de gramáticas, las cuales coinciden con las ya presentadas en la tabla (4). Una gramática G=(V,T,P,s₀) se dice ser

irrestricta

si $P\subset V^+\times (V\cup T)^*$, es decir, las producciones de la gramática tienen como antecedentes palabras no-vacías de símbolos variables,

sensible al contexto con borro

si las producciones de la gramática son de la forma $\sigma A\tau\rightarrow \sigma \alpha\tau$, donde $A\in V$ y $\alpha,\sigma,\tau\in(V\cup T)^*$,

sensible al contexto

si las producciones de la gramática son de una cualquiera de las formas siguientes,

1.

$\sigma A\tau\rightarrow \sigma \alpha\tau$, donde $A\in V$, $\sigma,\tau\in(V\cup T)^*$ y $\alpha\in(V\cup T)^+$,

2.

$s_0\rightarrow \mbox{\it nil\/}$,

y además s₀ no aparece como consecuente en ninguna producción,

libre de contexto

si las producciones de la gramática son de la forma $A\rightarrow \alpha$, donde $A\in V$ y $\alpha\in(V\cup T)^*$,

LR(k)

si la gramática es libre de contexto y además satisface las restricciones enunciadas a continuación. i) El símbolo inicial no se deriva de sí mismo mediante reglas que preserven la longitud de palabras derivadas. ii) Para cualesquiera variables $A_1,A_2\in V$ y cualesquiera palabras $\sigma_1,\sigma_2,\tau_1,\tau_2\in (V+T)^*$ y $\upsilon_1,\upsilon_2\in T^*$ rige la implicación siguiente:

$$\left.\begin{array}{c} \begin{array}{rclrcl} S &\stackrel{*... ...igma_1 &=& \sigma_2 \\ \tau_1 &=& \tau_2 \end{array}\right.$$

donde para cada palabra $\sigma$ denotamos por $\left.\sigma\right\vert _{n}$ al mayor prefijo de $\sigma$ con longitud a lo sumo n.

LL(k)

si la gramática es libre de contexto y además satisface la restricción enunciada a continuación. Para cualquier variable $A_1\in V$ y cualesquiera palabras $\tau_1,\tau_2,\upsilon_1,\upsilon_2\in (V+T)^*$ y $\sigma,\phi_1,\phi_2\in T^*$ rige la implicación siguiente:

$$\left.\begin{array}{c} \begin{array}{rclrclrcl} S &\stackre... ...k} \end{array}\right\} \ \ \ \Rightarrow\ \ \ \tau_1=\tau_2.$$

Las gramáticas del tipo LL(k) o LR(k) se dicen ser gramáticas libres de contexto deterministas.

lineal

si las producciones de la gramática son de la forma $A\rightarrow \alpha B \beta$ o $A\rightarrow \alpha$, donde $A,B\in V$ y $\alpha,\beta\in T^*$,

lateral

si las producciones de la gramática son todas de la forma $A\rightarrow \alpha B$ o $A\rightarrow \alpha$, donde $A,B\in V$ y $\alpha,\beta\in T^*$, en cuyo caso la gramática es derecha, o bien son todas de la forma $A\rightarrow B \alpha$ o $A\rightarrow \alpha$, en cuyo caso la gramática es izquierda.

Puede verse que las clases de gramáticas así definidas forman una jerarquía en el siguiente sentido:

$$\left.\begin{array}{c} \mbox{\it lineal derecha\/} \\ \Upd... ...x{\it SCB\/} & \Rightarrow & \mbox{\it tipo 0\/} \end{array}$$

Cada una de las implicaciones mostradas es estricta pues sus recíprocos no son válidos según lo atestiguan contraejemplos apropiados que iremos presentando a lo largo de este curso. Un lenguaje L se dice ser del mismo tipo que una gramática que lo genere. Para concluir esta sección presentamos en la proposición siguiente una manera de re-escribir gramáticas que será de utilidad posteriormente.

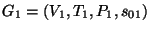
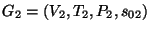
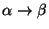
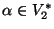
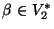
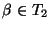
Proposición 4.1   Para toda gramática $G_1=\left(V_1,T_1, P_1,s_{01}\right)$ y exite una gramática equivalente $G_2=\left(V_2,T_2, P_2,s_{02}\right)$, con el mismo conjunto de símbolos terminales T₂=T₁, tal que en la nueva gramática las producciones son de la forma $\alpha\rightarrow\beta$, donde $\alpha\in V_2^*$, y bien $\beta\in V_2^*$ o bien $\beta\in T_2$, es decir, consta de un único símbolo terminal. Además, la gramática G₂ es del mismo tipo que la gramática G₁.

En efecto, dada $G_1=\left(V_1,T_1, P_1,s_{01}\right)$, para cada símbolo terminal $t\in T_1$, sea v_t un nuevo símbolo variable. Hagamos $V_2=V_1\cup \{v_t\vert t\in T_1\}$, s₀₂=s₀₁ y en el conjunto de produciones P₂ colocamos cada una de las producciones en P₁, habiendo sutituído toda aparición de caracteres $t\in T_1$ por sus respectivos $v_t\in V_2$, más las producciones de la forma $v_t\rightarrow t$. Por un lado, G₁ está subsumida por G₂ pues toda derivación en G₁ da una derivación en G₂ y, por otro lado, de la observación (2.3.1) se sigue que G₂ está subsumida por G₁. Es claro que la gramática G₂ es del mismo tipo que G₁.
Siguiente: Ejercicios Un nivel arriba: Gramáticas formales Anterior: Ejemplos