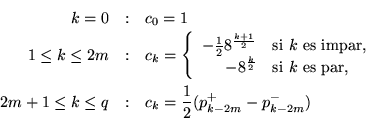


Siguiente: .
Un nivel arriba: Ecuaciones diofantinas cuadráticas (EDC)
Anterior: .
El siguiente procedimiento es similar al anterior.
Sea
 una instancia de 3SAT de m cláusula y n variables. Supondremos que
una instancia de 3SAT de m cláusula y n variables. Supondremos que  no posee cláusulas repetidas ni tautologías. Enumeremos al conjunto de clásusulas como
no posee cláusulas repetidas ni tautologías. Enumeremos al conjunto de clásusulas como
Hagamos
y para cada variable Xj
Sea q=2m+n. Para cada
![$k\in [0,q]$](img1884.gif) definimos:
definimos:
Hagamos
Existen 1+q coeficientes
tales que
Tomemos los q primos consecutivos
 a partir de P0=13.
Para cada
a partir de P0=13.
Para cada
![$k\in [0,q]$](img1884.gif) elegimos
elegimos 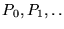 como el mínimo entero que satisface el sistema de congruencias
como el mínimo entero que satisface el sistema de congruencias
Definimos los coeficientes
Consideramos entonces la instancia del problema (EC) siguiente:
Guillermo Morales-Luna
2000-07-10
 una instancia de 3SAT de m cláusula y n variables. Supondremos que
una instancia de 3SAT de m cláusula y n variables. Supondremos que ![$k\in [0,q]$](img1884.gif) definimos:
definimos:
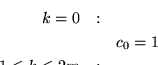
 a partir de P0=13.
Para cada
a partir de P0=13.
Para cada
![$k\in [0,q]$](img1884.gif) elegimos
elegimos