



Siguiente: Cambios de mapas
Arriba: Variedades diferenciables
Anterior: Variedades diferenciables
Mapas y atlas admisibles. Isomorfismos
La palabra ``mapa'' se traduce al francés por carte, al alemán por karte,
al inglés por chart. Lo mencionamos para evitar toda confusión con la
voz inglesa mapping que significa ``aplicación''.
Teorema 1.1
Toda variedad topológica es un espacio localmente conexo.
Demostración
Sean 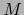 una variedad topológica y
una variedad topológica y 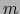 un punto arbitrario de
un punto arbitrario de 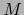 .
Debemos probar que toda vecindad de
.
Debemos probar que toda vecindad de 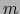 contiene una vecindad conexa de
contiene una vecindad conexa de 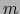 .
.
Sea, pues, 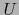 una vecindad arbitraria del punto
una vecindad arbitraria del punto 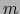 en
en 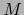 .
Por hipótesis, existe un mapa
.
Por hipótesis, existe un mapa 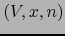 de
de 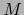 en el punto
en el punto 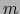 .
. 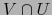 es también una vecindad de
es también una vecindad de 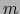 . Basta mostrar que
. Basta mostrar que 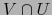 contiene una
vecindad conexa de
contiene una
vecindad conexa de 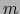 . Ahora bien
. Ahora bien 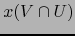 es una vecindad del punto
es una vecindad del punto
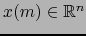 contenida en el abierto
contenida en el abierto 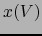 de
de
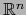 . Dicha
vecindad
. Dicha
vecindad 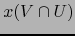 contiene una bola abierta
contiene una bola abierta 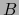 (para una norma
arbitrariamente fijada sobre
(para una norma
arbitrariamente fijada sobre
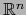 ) de centro
) de centro 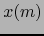 . Luego
. Luego
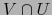 contiene
contiene 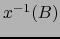 una vecindad conexa de
una vecindad conexa de 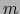 en
en 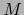 .
.

Teorema 1.2
Toda variedad topológica separada es un espacio localmente compacto.
Demostración
Sea 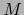 una variedad topológica separada y
una variedad topológica separada y 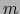 un punto arbitrario de
un punto arbitrario de 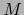 .
.
Debemos probar que 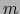 posee una vecindad compacta.
posee una vecindad compacta.
Sea 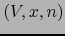 un mapa
de
un mapa
de 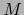 en el punto
en el punto 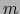 .
.
El abierto 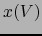 de
de
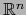 es una vecindad
del punto
es una vecindad
del punto
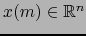 .
. 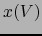 contiene, pues, una bola cerrada
contiene, pues, una bola cerrada
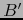 (para una norma arbitraria en
(para una norma arbitraria en
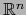 ) de radio positivo,
de centro
) de radio positivo,
de centro 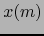 . El conjunto
. El conjunto
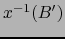 es una vecindad de
es una vecindad de 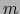 con respecto a
con respecto a 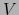 , luego, por ser
, luego, por ser 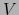 abierto, también con respecto
a
abierto, también con respecto
a 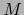 . Dicha vecindad
. Dicha vecindad
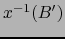 es compacta.
es compacta.

Nota
Citemos sin prueba el siguiente teorema del que se puede decir que
pertenece a la ``cultura general'' matemática. Se demuestra generalmente
por métodos de topología algebraica y se debe al matemático
holandés LIUTZEN E. J. BROUWER.
Una consecuencia importante de este resultado es el siguiente:
Teorema 1.4 (de la
INVARIANCIA DE LA DIMENSIÓN)
Sea 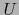 un abierto no vacío de
un abierto no vacío de
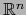 . Si existe un
homeomorfismo
. Si existe un
homeomorfismo 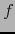 de
de 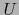 sobre un conjunto abierto
sobre un conjunto abierto 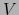 de
de
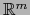 , vale necesariamente:
, vale necesariamente:
Demostración
Por simetría cabe suponer 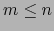 . Adoptando esta hipótesis podemos
escribir:
. Adoptando esta hipótesis podemos
escribir:
Identificamos
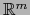 con el subespacio
con el subespacio
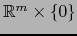 de
de
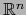 . De conformidad con ello, consideramos
. De conformidad con ello, consideramos 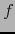 como una aplicación
continua e inyectiva del abierto
como una aplicación
continua e inyectiva del abierto 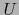 de
de
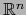 en
en
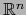 . Por
el teorema de la invariancia del recinto
. Por
el teorema de la invariancia del recinto 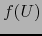 es también un abierto no
vacío de
es también un abierto no
vacío de
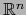 . Por lo tanto no puede estar contenido en un
subespacio propio de
. Por lo tanto no puede estar contenido en un
subespacio propio de
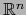 . Así pues, necesariamente
. Así pues, necesariamente 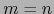 .
.

Subsections




Siguiente: Cambios de mapas
Arriba: Variedades diferenciables
Anterior: Variedades diferenciables
Guillermo M. Luna
2009-06-14
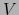 es un espacio abierto de
es un espacio abierto de 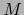 tal que existe un homeomorfismo
de
tal que existe un homeomorfismo
de 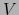 sobre un abierto
sobre un abierto 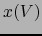 de
de
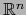 , la terna
, la terna 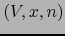 se
dice que es un MAPA DE DIMENSIÓN
se
dice que es un MAPA DE DIMENSIÓN 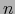 de
de 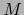 .
. 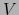 se llama el DOMINIO DEL MAPA considerado.
se llama el DOMINIO DEL MAPA considerado.
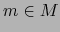 . Un mapa
. Un mapa 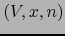 de
de 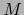 se dice que es un MAPA EN EL PUNTO
se dice que es un MAPA EN EL PUNTO 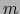 de
de 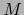 si
si 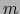 pertenece al dominio
pertenece al dominio 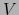 de dicho mapa.
de dicho mapa.
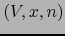 un mapa de
un mapa de 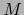 .
.
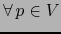 , escribamos:
, escribamos:

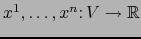 se llaman las
COORDENADAS LOCALES o simplemente las COORDENADAS RELATIVAS AL MAPA
se llaman las
COORDENADAS LOCALES o simplemente las COORDENADAS RELATIVAS AL MAPA 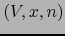 . Nuestra notación será:
. Nuestra notación será:
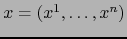 .
.
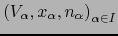 de mapas de
de mapas de 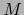 (si existe) se dice que es un ATLAS de
(si existe) se dice que es un ATLAS de 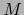 si
si
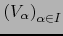 es un recubrimiento de
es un recubrimiento de 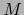 , es
decir
, es
decir
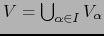 .
.
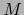 se dice que es una VARIEDAD TOPOLÓGICA, si
posee un atlas. Equivalentemente:
se dice que es una VARIEDAD TOPOLÓGICA, si
posee un atlas. Equivalentemente:
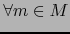 existe un mapa de
existe un mapa de
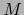 en el punto
en el punto 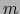 .
.