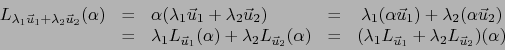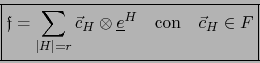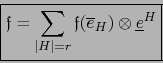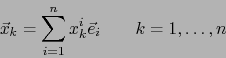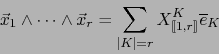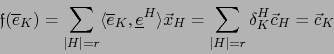



Siguiente: Producto exterior de formas
Arriba: Aplicaciones multilineales alternadas. Formas
Anterior: Aplicación dual de una
Recordemos el siguiente resultado elemental de álgebra lineal.
Mediante dicho isomorfismo canónico convenimos en identificar los espacios vectoriales
 . Escribimos simplemente:
. Escribimos simplemente:
Demostración
- Patentemente
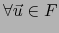 la aplicación
la aplicación 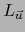 es lineal, o sea,
es lineal, o sea,
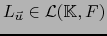 .
.
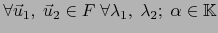 vale:
vale:
o sea:
Así pues, la aplicación
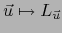 es una aplicación lineal de
es una aplicación lineal de 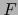 en
en
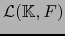 .
.
- Supongamos que
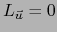 , vale decir
, vale decir
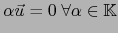 . Al tomar en particular
. Al tomar en particular 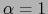 , obtenemos
, obtenemos  . Esto muestra que la aplicación lineal
. Esto muestra que la aplicación lineal
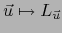 es
inyectiva.
es
inyectiva.
- Sea
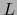 una aplicación arbitraria de
una aplicación arbitraria de
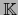 en
en 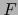 , elemento de
, elemento de
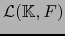 . Definamos
. Definamos
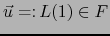 .
.
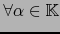 se cumple:
se cumple:
luego 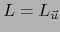 . Así pues, la aplicación lineal
. Así pues, la aplicación lineal
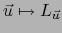 es superyectiva.
es superyectiva.

Definición 4.1
Sean  espacios vectoriales;
espacios vectoriales;  de dimensión finita.
de dimensión finita.
 los elementos del espacio vectorial
los elementos del espacio vectorial
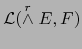 (es decir, aplicaciones lineales
(es decir, aplicaciones lineales
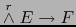 ) se llaman FORMAS EXTERIORES VECTORIALES DE GRADO SOBRE EL ESPACIO VECTORIAL , DE VALORES EN .
) se llaman FORMAS EXTERIORES VECTORIALES DE GRADO SOBRE EL ESPACIO VECTORIAL , DE VALORES EN .
Observación
Por el convenio que precede:
Es decir: Las forma exteriores de grado cero sobre  , de valores en
, de valores en 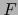 , son simplemente elementos de
, son simplemente elementos de 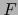 .
.
Observación
Por el teorema 2.3.1 vale:
Así pues las ``formas exteriores escalares'' que estudiamos hasta el momento son un caso particular de formas exteriores vectoriales.
Observación
Por el teorema 2.1.7 vale la identificación:
Explícitamente todo elemento
 puede identificarse con la aplicación
puede identificarse con la aplicación
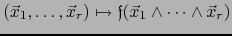 que es una aplicación
que es una aplicación 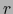 -lineal alternada
-lineal alternada 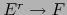 .
.
Teorema 4.2
Sea
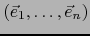 una base de E. Sean
una base de E. Sean
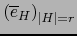 y
y
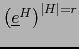 las bases asociadas de sendos espacios vectoriales
las bases asociadas de sendos espacios vectoriales
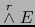 y
y
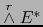 . Toda forma exterior vectorial
. Toda forma exterior vectorial
 puede representarse únicamente como:
Más precisamente, vale:
puede representarse únicamente como:
Más precisamente, vale:
Demostración
- Sea
 . Definamos
. Definamos
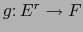 por:
por:
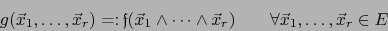 |
(1) |
Si
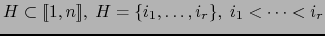 vale
en particular:
vale
en particular:
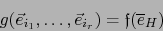 |
(2) |
Para vectores arbitrarios
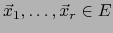 escribamos:
escribamos:
e introduzcamos la matriz
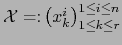 de tipo
de tipo  .
.
Por el teorema 2.1.3 y la relación (2) se verifica:
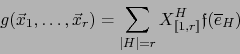 |
(3) |
donde
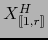 son los menores de orden
son los menores de orden 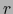 de la matriz
de la matriz 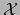 .
.
En virtud de (1), la relación (3) equivale a:
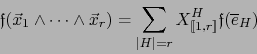 |
(4) |
Pero por el teorema 1.4.18:
de donde, siendo la base
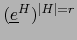 la dual de la base
la dual de la base
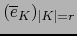 :
:
Llevando esto a (4), conseguimos:
Ya que los elementos descomponibles engendran
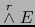 , la relación (5) entraña la fórmula enunciada:
, la relación (5) entraña la fórmula enunciada:
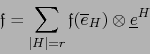 |
(6) |
- Queda por probar que (6) es la única representación:
 |
(7) |
Pero si
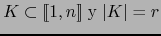 , obtenemos sin más de (7):
, obtenemos sin más de (7):

Subsections




Siguiente: Producto exterior de formas
Arriba: Aplicaciones multilineales alternadas. Formas
Anterior: Aplicación dual de una
Guillermo M. Luna
2009-06-14
![]() . Escribimos simplemente:
. Escribimos simplemente: