Puesto que ![]() , subvariedad abierta de
, subvariedad abierta de ![]() con su estructura
canónica, es una variedad
con su estructura
canónica, es una variedad ![]() , podemos hablar de la
diferenciabilidad de la curva
, podemos hablar de la
diferenciabilidad de la curva ![]() en
en ![]() según la definición 5.2.1. Usando los mapas admsibles
según la definición 5.2.1. Usando los mapas admsibles
![]() de
de ![]() en
en ![]() y
y ![]() de
de
![]() en
en ![]() vemos que:
vemos que:
La curva ![]() es diferenciable (como diremos por comodidad) EN EL TIEMPO , si y sólo si la curva
es diferenciable (como diremos por comodidad) EN EL TIEMPO , si y sólo si la curva
![]() en el abierto
en el abierto
![]() de
de
![]() es diferenciable C.D. (o sea derivable) en el tiempo
es diferenciable C.D. (o sea derivable) en el tiempo
![]() .
.
Consideraciones heurísticas
Sea ![]() un espacio afín de dimensión finita y
un espacio afín de dimensión finita y ![]() su espacio
vectorial asociado. Sea
su espacio
vectorial asociado. Sea
![]() una curva en
una curva en ![]() diferenciable en el tiempo
diferenciable en el tiempo ![]() . Se sabe que el vector derivada:
. Se sabe que el vector derivada:
Deseamos generalizar esta definición sustituyendo el espacio ![]() por una variedad diferenciable
por una variedad diferenciable ![]() . Evidentemente la fórmula (17)
carece de sentido en este caso, pero es natural definir
. Evidentemente la fórmula (17)
carece de sentido en este caso, pero es natural definir ![]() como un vector conveniente del espacio vectorial tangente
como un vector conveniente del espacio vectorial tangente
![]() . Para encontrar un candidato adecuado volvemos al
espacio afín
. Para encontrar un candidato adecuado volvemos al
espacio afín ![]() de dimensión finita y nos fijamos en el
vector del espacio tangente
de dimensión finita y nos fijamos en el
vector del espacio tangente
![]() que se identifica
con el vector
que se identifica
con el vector
![]() . Éste es la funcional
. Éste es la funcional
![]() , la derivada según el vector
, la derivada según el vector ![]() en el punto
en el punto ![]() .
.
Usando la regla de la cadena (teorema 4.4.4) obtenemos
![]() :
:
En vista de la adaptación a variedades con bordes conviene previamente hacer algo más generales nuestras consideraciones heurísticas.
Llamaremos CURVA EN EL SEMIPLANO CERRADO
![]() a
una aplicación continua
a
una aplicación continua
![]() , donde
, donde
![]() es un intervalo arbitrario (no necesariamente abierto) en
es un intervalo arbitrario (no necesariamente abierto) en ![]() . Si
. Si
![]() contiene uno o dos extremos,
contiene uno o dos extremos, ![]() será una variedad con borde de
dimensión 1.
será una variedad con borde de
dimensión 1.
Sea ![]() . Decir que
. Decir que ![]() es diferenciable en el tiempo
es diferenciable en el tiempo ![]() significa según las definiciones 5.5.8 y 4.6.1:
significa según las definiciones 5.5.8 y 4.6.1:
Demostración
Por ser ![]() diferenciable en el tiempo
diferenciable en el tiempo ![]() y
y ![]() en el punto
en el punto
![]() , en virtud del teorema 5.5.7 la función
, en virtud del teorema 5.5.7 la función
![]() es diferenciable en
es diferenciable en ![]() . Equivalentemente: es
derivable en
. Equivalentemente: es
derivable en ![]() (C.D.).
(C.D.).
La funcional
![]() dada por:
dada por:
![]() está, pues, bien definida. La llamaremos
está, pues, bien definida. La llamaremos ![]() .
Debido al ``caso particular'' del teorema 4.3.6 son válidas las
siguientes comprobaciones:
.
Debido al ``caso particular'' del teorema 4.3.6 son válidas las
siguientes comprobaciones:
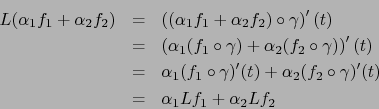
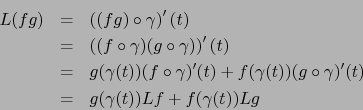
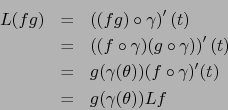
Observación
Las consideraciones heurísticas que preceden al teorema
6.1.8 garantizan la permanencia de la definición del vector
tangente ![]() .
.
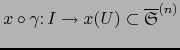 se
supone derivable en el tiempo
se
supone derivable en el tiempo
Demostración
![]() vale por definición
del isomorfsimo
vale por definición
del isomorfsimo
![]() :
: